【推荐平台】离线推荐算法——Random-Walk

1 背景

随着业务的不断发展，以及后疫情时代视频会议市场逐渐趋于稳定，目前，AI+社交成为公司下一个阶段的战略目标。ZRS（Zoom Relevant Service）通过多种方式导入用户业务数据，从0到1构建公司级准实时用户网络，为用户提供统一的搜索与推荐体验，助力高效社交。

2 现状

在ZRS中，我们提供实体之间的相关性/相似性分数。以用户实体为例：对于用户 ID 的输入查询，评分算法将为他/她/他们的相关联系人提供相应的相关性分数：

输入 – 用户0

输出 – {用户1:分数1，用户2:分数2，用户3:分数3…}

2.1 数据生产

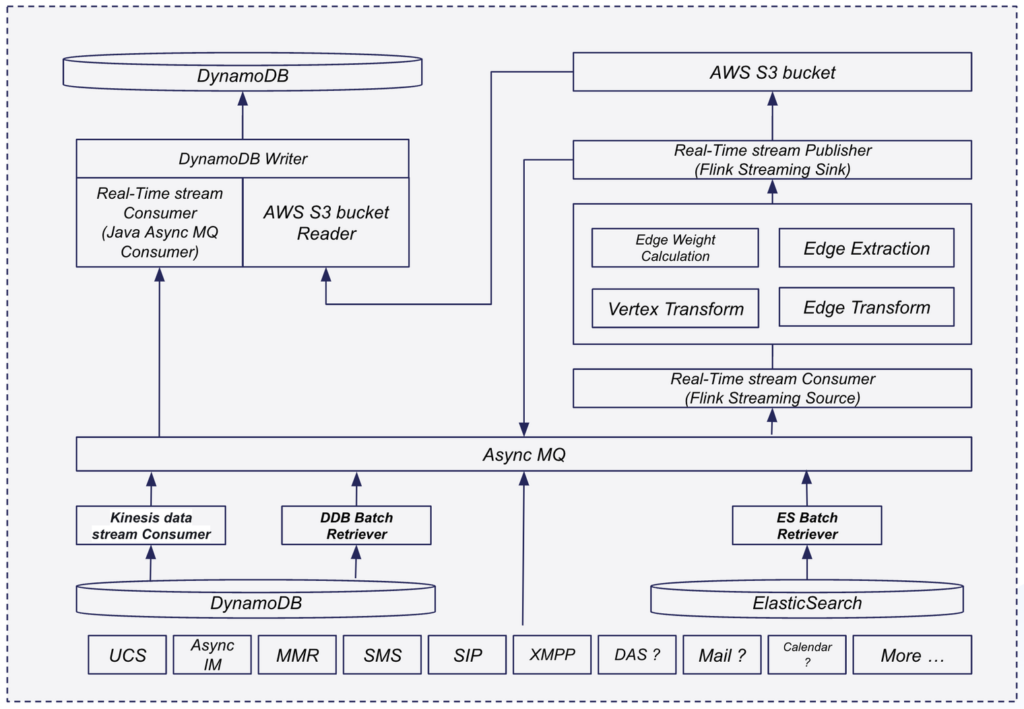
当前，ZRS的数据源主要来源于3部分，分别为业务实时数据库、ElasticSearch引擎，以及Amason S3存储。其中，业务实时数据库、ElasticSearch引擎的数据分别通过流式写入和批处理的方式导入Kafka队列，再由ZRS进行数据清洗与消费；通过配置Lambda函数，ZRS监听Amason S3存储变更，在文件被写入S3后，ZRS将其下载到本地，进行处理。

2.2 数据模型

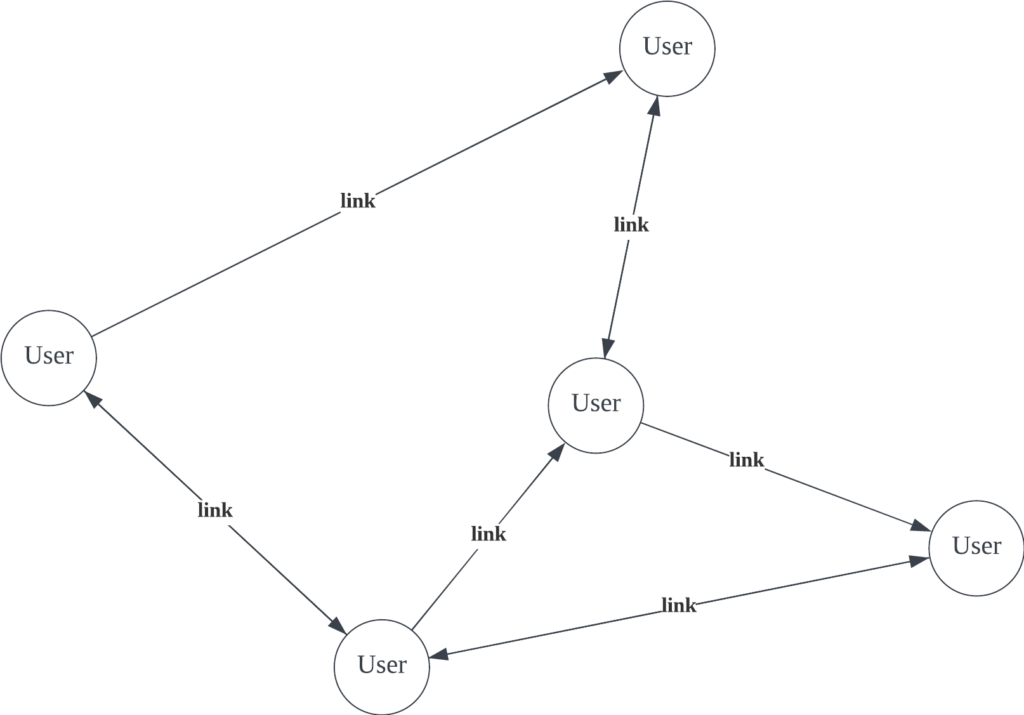
我们将用户关联关系抽象为有向图。其中，顶点对应不同的用户，边对应用户间的一种关联关系。有些关联关系是单向的，例如好友申请、联系人星标等；而有些关联关系是双向的，例如会议、聊天等。

我们为顶点和边分别存储，模式如下：

Primary Key	Range Key	Src_Obj_ID	Dst_Obj_ID	Attribute_1	Attribute_2	……
{edge__id}	{edge_type}	{src_obj_id}	{dst_obj_id}	{value}	{value}	……

边数据库 – DynamoDB

*Primary Key*	Range Key	Attribute_1	Attribute_2	Attribute_3	……
{object_id}	{object_type}	{value}	{value}	{value}	……

顶点数据库 – DynamoDB

2.3 服务接口

以推荐为例，客户端请求当前用户ID下的TOP50关联用户列表，API如下：

Request Headers:

Name	Value	Required
cookie	{zak,zm_aid,zm_haid }	Yes
x-zm-user-id	{userId}	Optional
…	…	…

Request Headers

Request Body:

{
    "size": 19,
    "hasSameAccount": true
}

Field Name	Field Type	Description
size	int	Get the number of user lists，Max size <= 500, default 100
hasSameAccount	Boolean	Only the userid of the same accountid is returned
offlineData	Boolean	use offline data? default false. Offline data improves accuracy, but there may be occasional data consistency issues due to update timeliness.

Request Body

Response Body:

{
    "success": true,
    "data": [
        {
            "userId": "K2ldnxjSTjy0QRkoODAYfQ",
            "score": 1.92
        },
        ...
    ],
    "totalSize": 6
}

Field Name	Field Type	Description
userId	String
score	float
pos	int	Sort Position

Response Body

2.4 基于权重的实时算法

算法配置如下（片段）：

- businessName: ChannelMember
  businessId: 1
  fieldMappingDetails:
    - fieldName: weight
      condition: greater
      value: 5
      weight: 1
- businessName: Star
  businessId: 3
  fieldMappingDetails:
    - fieldName: relevantUserId
      condition: exist
      weight: 1
- businessName: chat
  businessId: 4
  fieldMappingDetails:
    - fieldName: chatCounts
      condition: plugIn
      components: chatCountsPlugin

其中businessName和businessId标识了用户间关联关系的类型，对应边数据库中的{edge_type}；而fieldMappingDetails是一个列表，列表中的每一项对应一个attribute，分别定义了属性名chatCounts，条件condition，数值value和权重weight。

算法流程如下：

搜索Src_Obj_ID为该用户的所有边，并使用上述算法配置，计算每条边所对应的权重。
将边按照Dst_Obj_ID聚合，以聚合的粒度对第一步计算出来的权重进行求和，此即表示从Src_Obj_ID到Dst_Obj_ID两个用户间的连接强度绝对值。
为每个Dst_Obj_ID对应的用户，按照的连接强度的倒序进行排序，即可。

2.5 局限

实时算法的优势在于可以保证数据的准确性与及时性，但以牺牲算法的准确度为代价。由于ZRS需要保证接口SLA，实时算法无法承受较为复杂的业务逻辑，导致推荐结果准确度较低，具体体现为以下几个方面：

算法配置中的权重主要是依据经验，很难保证最优。
用户权重基于直接相连的边进行计算，但对于没有直接联系的用户，则无法计算关联关系，即使这两个用户拥有1/2以上共同好友。
计算时，只使用了图中的局部信息，没有基于全局的视角进行计算。例如，对于某些“明星用户”，他们与更多的人进行交流，是社交圈里的枢纽节点，针对这些用户，我们应当提高其作为推荐时的排名。

3 方案

3.1 PageRank与网页排名

PageRank 是Google 搜索用来在搜索引擎结果中对网页进行排名的算法。它的工作原理是通过计算页面链接的数量和质量来粗略估计网站的重要性。基本假设是更重要的网站可能会收到更多来自其他网站的链接。

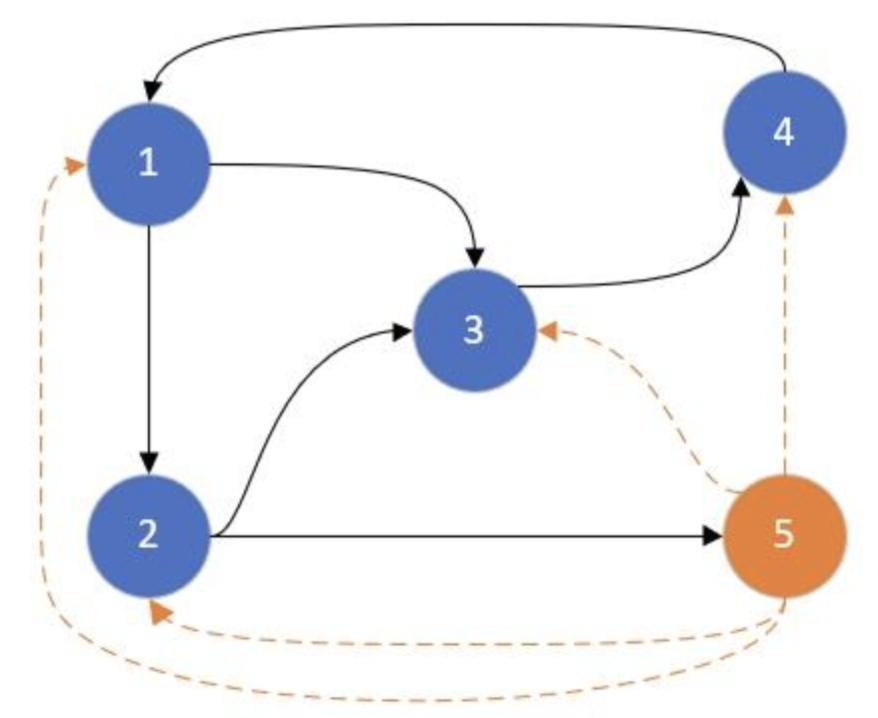
我们用一种朴素的方法来解释PageRank，在该模型中，我们使用一个图结构来描述Web，将该图记为G。G中的每个节点表示一个网页，节点与节点间的有向边表示网页间的超链接。上图描述了一个包含5个节点的简单图结构（忽略橙色虚线）。在图中，节点1指向了节点2与节点3，这表示网页1具有指向网页2和网页3的超链接。

在该模型中，我们再假设存在一个上网者Surfer，该Surfer在任一时刻停留在Web Graph中的某一个网页上，表示Surfer正在浏览当前网页。在下一时刻，Surfer必须从以下两个行动中选择一个执行：

1）行为1（Random Action）：从当前网页的所有超链接中随机选择一个，并点击该链接以访问下一个网页；

2）行为2（Jump Action）：在浏览器中新输入一个网址，然后访问其对应的网页。

我们让surfer一直重复这样的选择（即每次选择一个行动，跳转到下一个页面；然后又选择一个行动，再跳转到下一个页面），并记录该surfer对Web Graph中每个网页的访问次数。假设surfer前十次选择的节点序列是（1, 3, 4, 1, 2, 4, 1, 2, 5, 3）。在前十次选择中，节点1被访问的概率为0.3，节点2被访问的概率为0.2，节点3被访问的概率为0.2 ，节点4被访问的概率为0.2，节点5被访问的概率为0.1。如果我们一直让surfer游走下去，可以想象，这样的概率会逐渐趋于稳定，那么最终将得到每个节点的PageRank值。

3.2 ItemRank与电影推荐

ItemRank是基于经典推荐数据集MovieLens来设计的。它直觉上的动机是：如果我们能够构建出电影与电影之间的关系图，并且图中的边表征电影间的相似性，那么用户对电影的偏好可以在这个图中进行传播。

这样的表述与3.1存在不一致：3.1是用随机游走模型来解释PageRank的，没提过“传播”。其实我们也可以把PageRank看作为一种分值传播模型：可以理解为算法将每一个Web网页的PageRank值沿链接向外进行传播。随机游走模型中的行为1（Random Action）和行为2（Jump Action）定义了分值传播的规则。因此”分值传播”是理解PageRank的另外一种方式。

如何定义电影之间的关系呢？考虑到如果有大量用户既看过电影A也看过电影B，那么A与B可能存在某种相关性，我们可以为电影A与B之间添加一条边，边的权重就是用户的数量。通过这种方式，我们就可以构建出一张无向加权图。

有了这样一个图，我们可以将一个用户想象成随机游走者，TA从TA看过的电影出发，在图中游走。为了防止其走的过远（想象这样一个场景，偏好喜剧的观众，TA大概率不希望推荐恐怖片，但是，肯定有观众同时看了喜剧与恐怖片），我们修改2.1中的2个行为：

1）行为1（Random Action）：从当前电影的所有相关联的电影中，按照权重随机选择一个；

2）行为2（Reset Action）：随机回到TA看过的任意一个电影。

最后在多次游走后，我们得到TA对每部电影访问的概率，以此对电影从高到低排序即可得到推荐结果（去除TA看过的）。

3.3 Random-Walk-with-Restart与社交网络（Alberto 等人，2019）

ZRS中，用户之间的关系可以用同构的多层图模型来表示。其中，每一层代表一个维度下的关联关系，例如会议、聊天、电话等。不同层间编号相同的两个节点都表示同一个用户，他们之前相互连接（图中未画出）。

3.3.1 单层图的重启随机游走算法

让我们首先考虑仅有一层图模型 $G=(V,E)$ 与邻接矩阵 $A$ 的情况。假想游标从初始用户0 $v_0\in{V}$ 开始随机游走，考虑到时间是离散的，在第 $t$ 步，游标位于用户t $v_t\in{V}$ ，在下一步，它从 $v_t$ 走到 $v_{t+1}$ 。因此，我们可以认为：$\forall{x,y\in{v}}, \ \forall{t\in\mathbb{N}}$

$$
\mathbb{P}(v_{t+1}=y \vert v_t=x)=
\begin{cases}
\frac{w_{xy}}{\sum_{i=1}^{v}w_{xi}}, & \forall{x,y\in{E}}, \\
0, & \text{otherwise}.
\end{cases}
$$

其中 $w_{xy}$ 是图 $G$ 中从用户x到用户y的边所对应的权重。定义 $p_t(v)$ 作为游标在时间 $t$ 处在用户v的概率，我们可以描述概率分布 $P_t=(p_t(v))_{v\in{V}}$ 的演化：

$$
P_{t+1}^T=MP_t^T
$$

其中 $M$ 表示转换矩阵，它是 $A$ 的列归一化后的分布。方程 $P^T=MP^T$ 的解（如果存在的话），表示游标在无限时间内位于特定用户的概率。

我们引入重启的概念，在每次迭代时，游标还可以以固定概率 $r\in(0,1)$ 跳转到图中任意随机选择的节点来重新启动，这避免了行走陷入死胡同，并保证了平稳分布的存在。此外，我们可以将游标的重新启动限制在特定用户，称为种子。这样做时，游标将探索以种子用户邻域为中心的图，并且最终的概率分布可以被视为种子用户与图中所有其他用户之间的接近度。形式上，单层图的随机游走方程可以定义为：

$$
P_{t+1}^T=(1-r)MP_t^T+rP_0^T
$$

向量 $P_0$ 是初始概率分布。因此，在 $P_0$ 中，只有单一种子用户的值为1。经过多次迭代后，向量之间的差异 $P_{t+1}$ 和 $P_t$ 变得可以忽略不计，最终达到平稳概率分布。

3.3.2 多层同构图的重启随机游走算法

多重图是L个有向图的集合，每个有向图被视为一层，每层n个节点，对应全局n个用户。多层图 $G_M=(V_M,E_M)$ 的邻接矩阵 $A$ 为各层邻接矩阵的集合，定义如下：

$$
A=A^{[1]},\dots,A^{[L]}
$$

$$
V_M=\left\{{v_i^\alpha, \ i=1,\dots,n, \ \alpha=1,\dots,L}\right\}
$$

$$
E_M=
\left\{{(v_i^\alpha, v_j^\alpha), \ i,j=1,\dots,n, \ \alpha=1,\dots,L, \ A^{[\alpha]}(i,j)\neq{0}}\right\}
\cup
\left\{{(v_i^\alpha, v_i^\beta), \ i=1,\dots,n, \ \alpha\neq\beta}\right\}
$$

游标从层α下的用户 $v_i^\alpha$ 开始随机游走，下一个时刻可以走到层内的任何邻居用户，也可以走到层β下的当前用户 $v_i^\beta$ ，从而实现层间跳转。

因此，我们可以通过构建 nL × nL 矩阵 $A$ ，将单层图下的 RWR 算法扩展到多层图。矩阵 $A$ 包含游标在每一步可以遵循的不同类型的转换，定义为：

$$
A=
\begin{pmatrix}
(1-\delta)A^{[1]} & \frac{\delta}{L-1}I & \cdots & \frac{\delta}{L-1}I \\
\frac{\delta}{L-1}I & (1-\delta)A^{[2]} & \cdots & \frac{\delta}{L-1}I \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\delta}{L-1}I & \frac{\delta}{L-1}I & \cdots & (1-\delta)A^{[L]} \\
\end{pmatrix}
$$

其中 I 是 n × n 单位矩阵， $A^{[\alpha]}$ 是层α的邻接矩阵。对角线中的元素表示潜在的层内行走，而非对角线元素则说明不同层之间可能的跳跃。参数 $\delta\in(0,1)$ 对停留在层中或在层之间跳跃的概率进行量化。如果 $\delta=0$ ，在不考虑重新启动的情况下，游标将始终停留在同一层。

通过对 $A$ 进行列归一化，我们可以得到转换矩阵 $M$ 。多层图的随机游走方程可以定义为：

$$
{\overline{P}}_{t+1}^T=(1-r)M{\overline{P}}_t^T+r{\overline{P}}_{RS}^T
$$

其中， ${\overline{P}}_t^T=\left[P_t^1,\dots,P_t^L\right], \ t\in\mathbb{N}$ 是 n × L 向量，表示多层图中游标的概率分布。这些向量由每一层的概率分布组成。重启向量 ${\overline{P}}_{RS}^T$ 表示初始概率分布，我们将其定义为 ${\overline{P}}_{RS}=\tau{\overline{P}}_0$ 。其中向量参数 $\tau=\left[\tau_1,\dots,\tau_L\right]$ 代表多层图中每层的种子重新启动的概率，可以通过修改参数 $\tau_l$ 来调整每一层的重要性。

当达到平稳概率分布时，通过计算游标在所有层的所有用户的停留概率的几何平均值，即可计算出种子用户与图中所有其他用户之间的接近度。几何平均值惩罚某一层中接近度较高，但其余层中接近度较低的用户。

4 实现

我们基于pyspark，在databricks平台进行数据处理。

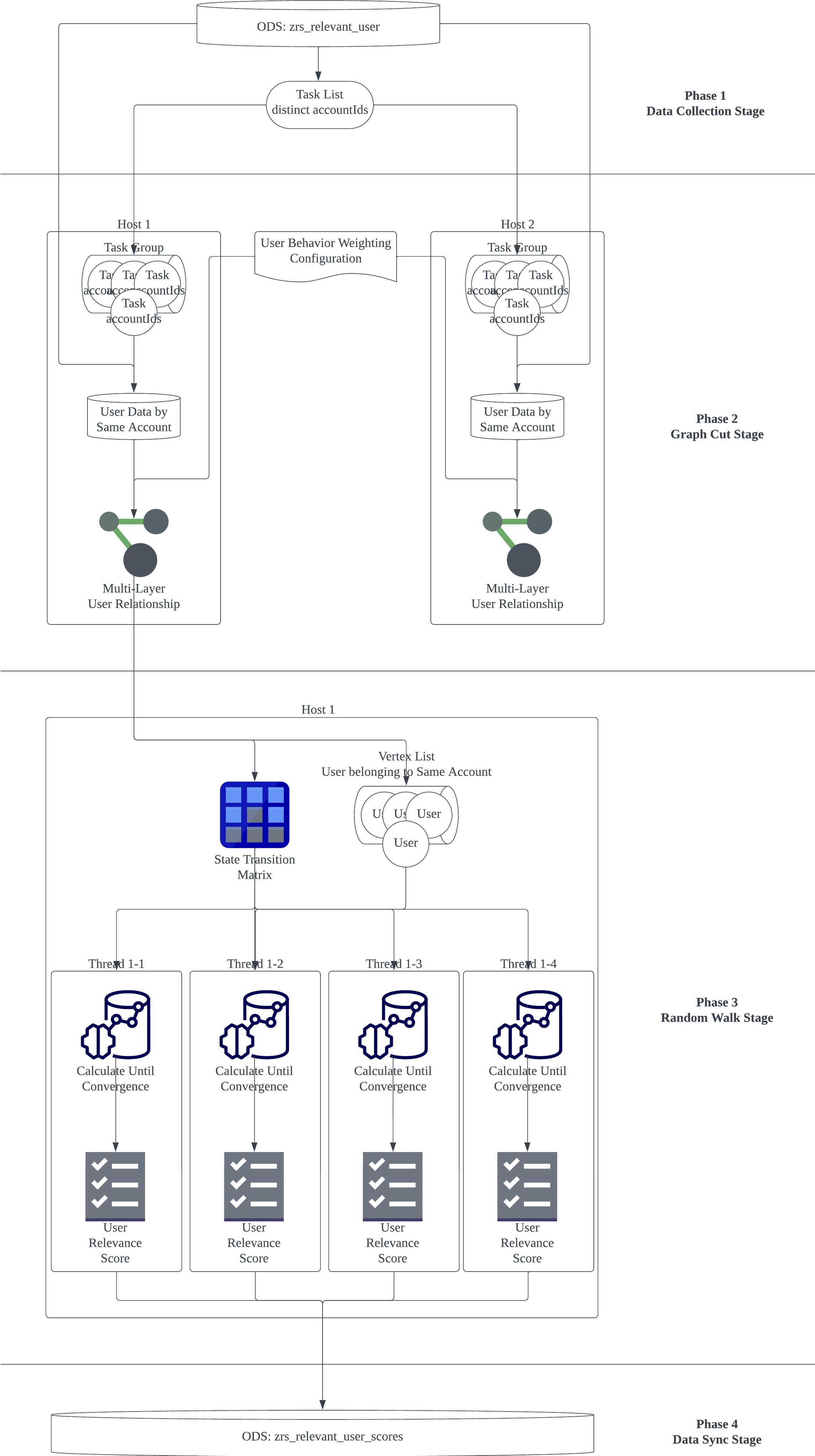
4.1 各阶段概览

如图所示，数据处理任务分为以下四个阶段：

数据导入：将用户数据导入databricks平台。
多层图构建：将用户数据按照账户粒度进行分组，按照预先定义的配置文件，为用户间的行为计算权重，作为算法中各层节点之间边的权重，构建多层图。
算法执行：根据2中的图，构建转移矩阵M，并遍历每一个用户，执行多层图的RWR算法，生成最终的结果
数据写入：将最终的结果写入在线存储。

4.2 多层图构建

4.2.1 计算边权重

在这一步中，我们要做的是根据relevantType，将不同类型的行为日志聚合为权重，输入输出如下所示：

accountId	userId	relevantAccountId	relevantUserId	relevantType	__extra_fields_examples
aid1	uid11	aid1	uid12	Meeting	7DaysMetting: 130DaysMetting: 3
aid1	uid11	aid2	uid21	Meeting	7DaysMetting: 030DaysMetting: 1
aid1	uid11	aid1	uid13	Chat	7DaysChat: 3
aid2	uid21	aid2	uid22	Meeting	7DaysMetting: 130DaysMetting: 1
aid2	uid22	aid2	uid23	Meeting	7DaysMetting: 030DaysMetting: 1

输入schema

accountId	userId	relevantAccountId	relevantUserId	layerName	weight
aid1	uid11	aid1	uid12	Meeting	5
aid1	uid11	aid2 (external user)	uid21	Meeting	1
aid1	uid11	aid1	uid13	Chat	1

输出schema

代码如下：

def calculate_link_weight_with_chat_counts_plugin(datastr: str) -> float:
    if datastr is None:
        return 0.0
    data = json.loads(datastr)
    chat_map = {}
    dm_and_mention_map = {}

    for i in range(-7, 0):
        delta = datetime.timedelta(days=i)
        n_days = datetime.datetime.now() + delta
        day_time = n_days.strftime('%Y-%m-%d')
        chat_counts_map = data.get(day_time)
        if chat_counts_map is None:
            continue

        chat_map['reply'] = chat_map.get('reply', 0.0) + chat_counts_map.get('reply', 0.0)
        chat_map['mention'] = chat_map.get('mention', 0.0) + chat_counts_map.get('mention', 0.0)
        chat_map['direct'] = chat_map.get('direct', 0.0) + chat_counts_map.get('direct', 0.0)
        if i > -3:
            dm_and_mention_map['mention'] = dm_and_mention_map.get('mention', 0.0) + chat_counts_map.get('mention', 0.0)
            dm_and_mention_map['direct'] = dm_and_mention_map.get('direct', 0.0) + chat_counts_map.get('direct', 0.0)

    chat_score = 0.0
    if sum(chat_map.values()) > 0:
        chat_score += 1
    if dm_and_mention_map.get('mention', 0.0) > 0:
        chat_score += 1
    if dm_and_mention_map.get('direct', 0.0) > 0:
        chat_score += 1
    return chat_score


def calculate_link_weight_with_plugin(name: str, data: str) -> float:
    if name == 'chatCountsPlugin':
        return calculate_link_weight_with_chat_counts_plugin(data)
    else:
        return 0.0


@udf(returnType=DoubleType())
def calculate_link_weight(row: Row) -> float:
    row_data = row.asDict()
    relevant_type = int(row_data.get(FIELD_NAME_RELEVANT_TYPE, None))
    if relevant_type not in CONFIG_LINK_WEIGHT.keys():
        return 0.0
    score = 0.0
    for field_rule in CONFIG_LINK_WEIGHT.get(relevant_type)['fieldMappingDetails']:
        field_value = row_data.get(field_rule['fieldName'], None)
        if field_value is None:
            continue
        if field_rule['condition'] == 'greater':
            field_value = float(field_value)
            if field_value > field_rule['value']:
                score += field_rule['weight']
        elif field_rule['condition'] == 'exist':
            score += field_rule['weight']
        elif field_rule['condition'] == 'plugIn':
            score += calculate_link_weight_with_plugin(field_rule['components'], field_value)
    return score

def prepare_weight():
    df_all = spark.sql(f'select * from {TABLE_ZRS} where {IS_NOT_DELETED}')
    df_all = df_all.repartition(PARALLEL_NUM, FIELD_NAME_USER_ID)

    df_all = df_all.filter(df_all[FIELD_NAME_ACCOUNT_ID].isNotNull()).filter(df_all[FIELD_NAME_RELEVANT_ACCOUNT_ID].isNotNull()).filter(df_all[FIELD_NAME_USER_ID].isNotNull()).filter(df_all[FIELD_NAME_RELEVANT_USER_ID].isNotNull()).filter(df_all[FIELD_NAME_RELEVANT_TYPE].isNotNull())

    # todo: wait data
    df_edge = df_all.withColumn('relevantWeight', calculate_link_weight(struct([df_all[x] for x in df_all.columns])))
    df_edge = df_edge.withColumn(FIELD_NAME_LAYER, merge_layer(df_edge[FIELD_NAME_RELEVANT_TYPE]))

    df_edge = df_edge.groupby(
        [FIELD_NAME_ACCOUNT_ID, FIELD_NAME_USER_ID, FIELD_NAME_RELEVANT_ACCOUNT_ID, FIELD_NAME_RELEVANT_USER_ID,
         FIELD_NAME_LAYER]).agg(F.sum('relevantWeight').alias(FIELD_NAME_LINK_WEIGHT))
    df_edge = df_edge.filter(df_edge[FIELD_NAME_LINK_WEIGHT] > 0)

    df_edge.write.option("overwriteSchema", "true").mode('overwrite').saveAsTable(TMP_TABLE_EDGE)

其中，变量 CONFIG_LINK_WEIGHT 定义了各个事件的权重， CONFIG_LAYER_MERGE 定义 relevantType 和 graphLayer 的映射关系。

4.2.2 图的导出

这一步中，我们根据上文生成的边，使用 python 的 igraph 库，以 accountId 为粒度构建多层图。输入格式如下：

accountId	graph
aid1	binary_code
aid2	binary_code
aid3	binary_code

其中，graph列为序列化后的多层图对象。代码如下：

def create_graph_for_layer(layer_edges_list: list, df_vertex: set) -> Graph:
    df_vertex_dict = {}
    for i, v_name in enumerate(df_vertex):
        df_vertex_dict[v_name] = i

    edges_weight_list = []
    edges_direct_list = []
    for i in range(len(layer_edges_list)):
        edges_weight_list.append(layer_edges_list[i][2])
        edges_direct_list.append((df_vertex_dict[layer_edges_list[i][0]], df_vertex_dict[layer_edges_list[i][1]]))

    graph = Graph(directed=True)
    graph.add_vertices(len(df_vertex))
    graph.add_edges(edges_direct_list)
    graph.es['weight'] = edges_weight_list
    graph.vs['name'] = list(df_vertex)
    graph = graph.simplify(multiple=True, loops=False, combine_edges="sum")
    return graph


def generate_graph(edges: List[Dict[str, Any]]) -> dict[str, Graph]:
    df_edges = pd.DataFrame(edges, columns=[FIELD_NAME_ACCOUNT_ID, FIELD_NAME_USER_ID, FIELD_NAME_RELEVANT_ACCOUNT_ID,
                                            FIELD_NAME_RELEVANT_USER_ID, FIELD_NAME_LAYER, FIELD_NAME_LINK_WEIGHT])
    df_edges['fromId'] = df_edges.apply(lambda x: x[FIELD_NAME_ACCOUNT_ID] + SPLIT + x[FIELD_NAME_USER_ID], axis=1)
    df_edges['toId'] = df_edges.apply(
        lambda x: x[FIELD_NAME_RELEVANT_ACCOUNT_ID] + SPLIT + x[FIELD_NAME_RELEVANT_USER_ID], axis=1)
    df_edges = df_edges.drop(columns=[FIELD_NAME_ACCOUNT_ID, FIELD_NAME_USER_ID, FIELD_NAME_RELEVANT_ACCOUNT_ID,
                                      FIELD_NAME_RELEVANT_USER_ID])

    df_vertex = set()
    df_vertex.update(df_edges['fromId'].tolist())
    df_vertex.update(df_edges['toId'].tolist())

    # Group by FIELD_NAME_LAYER and process data
    grouped = df_edges.groupby(FIELD_NAME_LAYER)
    layers = {name: group[['fromId', 'toId', FIELD_NAME_LINK_WEIGHT]].values.tolist() for name, group in grouped}

    # Creating graph for each layer ...
    graphs = {layer_name: create_graph_for_layer(layer_edges_list, df_vertex) for layer_name, layer_edges_list in
              layers.items()}
    return graphs


@udf(returnType=BinaryType())
def build_graph(edges: List[Dict[str, Any]]) -> bytes:
    graphs_with_all_nodes = generate_graph(edges)
    return pickle.dumps(graphs_with_all_nodes)

def prepare_graph():
    df_edge = spark.sql(f'select * from {TMP_TABLE_EDGE}')
    df_edge = df_edge.repartition(PARALLEL_NUM, FIELD_NAME_ACCOUNT_ID)

    df_graph = (df_edge.groupBy(FIELD_NAME_ACCOUNT_ID).agg(F.collect_list(struct(
        [FIELD_NAME_ACCOUNT_ID, FIELD_NAME_USER_ID, FIELD_NAME_RELEVANT_ACCOUNT_ID, FIELD_NAME_RELEVANT_USER_ID,
         FIELD_NAME_LAYER, FIELD_NAME_LINK_WEIGHT])).alias(FIELD_NAME_EDGES))
                .withColumn(FIELD_NAME_GRAPH, build_graph(FIELD_NAME_EDGES)))
    df_graph = df_graph.select(FIELD_NAME_ACCOUNT_ID, FIELD_NAME_GRAPH)
    df_graph.write.option("overwriteSchema", "true").mode('overwrite').saveAsTable(TMP_TABLE_GRAPH)

4.3 RWR算法实现

4.3.1 用户分组

users <= 100	users > 100	users > 1,000	users > 10,000	users > 100,000	users > 250,000	users > 300,000
72,350,905 accounts	19,700 accounts	2,863 accounts	365 accounts	11 accounts	3 accounts	0 accounts

某集群下用户规模

上图为公司某集群下账户规模。可以看出，每个账户有1～30万不等的用户。在上一步中，我们得到了各个账户下的用户关联图。如果我们以账户为粒度进行RWR，显然会导致数据倾斜，严重时还可能耗尽计算资源。但如果我们按照账户粒度进行RWR，最坏情况下针对每个用户都需要重新加载一次连接图，这在图很大且用户量很多的情况下，无疑会额外产生很大的开销（实测会导致计算时间变为原先的4-5倍，并且频繁GC）。因此，我们预先加工如下的任务表：

accountId	userIds
aid1	[“uid1”, “uid2”, …, “uid2000”]
aid1	[“uid2001”, “uid2002”, …, “uid3485”]
aid2	[“uid1”, “uid2”, …, “uid55”]

任务表schema

其中，我们以accountId为粒度，遵循同一个account下2000个用户为一组，不同account下的用户处在不同组的规则，对用户进行分割。代码如下：

@udf(returnType=IntegerType())
def mod_user(user_id: str, m: int) -> int:
    return hash(user_id) % m

def prepare_user_group():
    df_edge = spark.sql(f'select * from {TMP_TABLE_EDGE}')
    df_edge = df_edge.repartition(PARALLEL_NUM, FIELD_NAME_ACCOUNT_ID)

    df_user = df_edge.select(FIELD_NAME_ACCOUNT_ID, FIELD_NAME_USER_ID).distinct()

    df_account = df_user.groupby([FIELD_NAME_ACCOUNT_ID]).agg(F.count(FIELD_NAME_USER_ID).alias('userCnt'))
    df_account = df_account.withColumn('groupNum', (F.col('userCnt') / DATA_GROUP_SIZE + 1).cast(IntegerType()))
    df_account = df_account.select(FIELD_NAME_ACCOUNT_ID, 'groupNum')
    df_user = df_user.join(df_account, on=[FIELD_NAME_ACCOUNT_ID], how='left')
    df_user = df_user.withColumn('groupId', mod_user(FIELD_NAME_USER_ID, 'groupNum'))

    df_group = df_user.groupBy([FIELD_NAME_ACCOUNT_ID, 'groupId']).agg(F.collect_list(FIELD_NAME_USER_ID).alias(FIELD_NAME_USER_GROUP))
    df_group = df_group.select(FIELD_NAME_ACCOUNT_ID, FIELD_NAME_USER_GROUP)
    df_group.write.option("overwriteSchema", "true").mode('overwrite').saveAsTable(TMP_TABLE_USER_GROUP)

4.3.2 算法迭代

在这个步骤中，我们为上文中的每个组中的所有用户，计算所有与其相关联的用户，输出如下：

accountId	results
aid1	{“aid1#uid1#aid1#uid4”:0.23, …}
aid1	…
aid2	…

结果表schema

代码如下：

def get_multi_layer_matrix(layers: dict[str, Graph], delta: float, layer_num: int) -> list:
    transfer_matrix_list = list()
    col_eye_list = list()
    for layer in layers.values():
        layer_transfer_matrix = layer.get_adjacency_sparse(attribute='weight').transpose()
        layer_transfer_matrix = layer_transfer_matrix.multiply(1 - delta)

        layer_sum_array = layer_transfer_matrix.sum(axis=0)
        layer_sum_array = np.array(layer_sum_array)[0]
        layer_sum_array += delta

        layer_reciprocal_array = diags(1.0 / layer_sum_array).tocsc()
        layer_transfer_matrix = layer_transfer_matrix.dot(layer_reciprocal_array)

        # fix: graph only has one layer
        # layer_col_eye = layer_reciprocal_array.multiply(delta / (layer_num - 1))
        layer_col_eye = layer_reciprocal_array.multiply(delta / layer_num)

        transfer_matrix_list.append(layer_transfer_matrix)
        col_eye_list.append(layer_col_eye)

    return [transfer_matrix_list, col_eye_list]


def get_transfer_matrix_index_name(layers: dict[str, Graph]) -> list[str]:
    for _, any_layer in enumerate(layers.values()):
        return [name for name in any_layer.vs["name"]]


def get_transfer_matrix_name_index(layers: dict[str, Graph]) -> dict[str, int]:
    for _, any_layer in enumerate(layers.values()):
        d = dict()
        for idx, name in enumerate(any_layer.vs["name"], start=0):
            d[name] = idx
        return d


def get_seed_position(seed: int, layer_num: int, dim_num: int) -> list:
    seed_position = np.zeros(shape=(dim_num, 1))
    seed_position[seed, 0] = 1.0 / layer_num

    seed_position_list = list()

    for i in range(0, layer_num):
        seed_position_list.append(seed_position)

    return seed_position_list


def cal_random_walk_with_matrix_block(transfer_matrix_list: list[csc_array], col_eye_list: list[csc_array],
                                      position: list[np.ndarray], restart_position: list[np.ndarray],
                                      restart_prob: float) -> list[np.ndarray]:
    l = len(transfer_matrix_list)
    res = []
    for _ in range(0, l):
        res.append(np.zeros(shape=position[0].shape, dtype=position[0].dtype))

    for i in range(0, l):
        for j in range(0, l):
            # fix: graph only has one layer
            # layer_col_eye = layer_reciprocal_array.multiply(delta / layer_num)
            mat = col_eye_list[j].dot(position[j])
            if i == j:
                mat += transfer_matrix_list[j].dot(position[j])
            res[i] += mat
        res[i] *= 1 - restart_prob
        res[i] += restart_position[i] * restart_prob
    return res


def cal_residue(position: list[np.ndarray], next_position: list[np.ndarray]) -> float:
    residue = 0.0
    for i in range(0, len(position)):
        residue += np.sum((position[i] - next_position[i]) ** 2)
    return np.sqrt(residue)


def rwr_single_seed(transfer_matrix_list: list[csc_array], col_eye_list: list[csc_array],
                    restart_position: list[np.ndarray], restart_prob: float, threshold: float,
                    max_iters: int) -> np.ndarray:
    prob_position = restart_position
    for i in range(max_iters):
        next_prob_position = cal_random_walk_with_matrix_block(transfer_matrix_list, col_eye_list, prob_position,
                                                               restart_position, restart_prob)
        residue = cal_residue(prob_position, next_prob_position)
        prob_position = next_prob_position
        if residue <= threshold:
            break

    final_position = np.zeros((len(prob_position[0]), 1))
    for layer_prob_position in prob_position:
        final_position += layer_prob_position
    final_position /= len(prob_position)
    return final_position


def run_rwr_task(src_index: int, src_name: str, transfer_matrix_index_name: list[str],
                 transfer_matrix_list: list[csc_array], col_eye_list: list[csc_array],
                 restart_position: list[np.ndarray], restart_prob: float, threshold: float, max_iters: int) -> dict[
    str, float]:
    rwr_state = rwr_single_seed(transfer_matrix_list, col_eye_list, restart_position, restart_prob, threshold,
                                max_iters)
    results = {}
    for j, dst in enumerate(transfer_matrix_index_name):
        if src_index == j:
            continue

        score = float(rwr_state[j][0])
        if score < DROPPED_SCORE:
            continue

        results[src_name + SPLIT + dst] = score
    return results


def build_graph_context(graph_binary: bytes) -> dict:
    graphs_with_all_nodes = pickle.loads(graph_binary)

    transfer_matrix_name_index = get_transfer_matrix_name_index(graphs_with_all_nodes)

    # Generating Multiplex Adjacency Matrix...
    layer_num = len(graphs_with_all_nodes.values())
    multi_layer_matrix = get_multi_layer_matrix(graphs_with_all_nodes, DELTA, layer_num)
    transfer_matrix_index_name = get_transfer_matrix_index_name(graphs_with_all_nodes)
    n = len(transfer_matrix_index_name)

    return {
        'layer_num': layer_num,
        'n': n,
        'transfer_matrix_index_name': transfer_matrix_index_name,
        'transfer_matrix_name_index': transfer_matrix_name_index,
        'transfer_matrix_list': multi_layer_matrix[0],
        'col_eye_list': multi_layer_matrix[1]
    }


def do_rw(account_id: str, user_id: str, graph_context: dict) -> dict[str, float]:
    seed = account_id + SPLIT + user_id
    index = graph_context['transfer_matrix_name_index'][seed]

    seed_position = get_seed_position(index, graph_context['layer_num'], graph_context['n'])

    result_in_batch = run_rwr_task(index, seed, graph_context['transfer_matrix_index_name'],
                                   graph_context['transfer_matrix_list'], graph_context['col_eye_list'],
                                   seed_position, R, DIFF_THRESHOLD, MAX_IERS)
    return result_in_batch


def single_rw(account_id: str, user_ids: list[str], graph_context: dict) -> dict[str, float]:
    results = dict()
    for user_id in user_ids:
        result_in_single = do_rw(account_id, user_id, graph_context)
        results.update(result_in_single)
    return results


@udf(returnType=MapType(keyType=StringType(), valueType=DoubleType()))
def random_walk_with_restart(row: Row) -> dict[str, float]:
    row_data = row.asDict()

    account_id = row_data[FIELD_NAME_ACCOUNT_ID]

    graph_context = build_graph_context(bytes(row_data[FIELD_NAME_GRAPH]))

    user_ids = row_data[FIELD_NAME_USER_GROUP]

    return single_rw(account_id, user_ids, graph_context)


    df_graph = spark.sql(f'select * from {TMP_TABLE_GRAPH}')
    df_group = spark.sql(f'select * from {TMP_TABLE_USER_GROUP}')
    df_graph = df_graph.repartition(PARALLEL_NUM, FIELD_NAME_ACCOUNT_ID)
    df_group = df_group.repartition(PARALLEL_NUM, FIELD_NAME_ACCOUNT_ID)

    df_score = df_group.join(df_graph, on=[FIELD_NAME_ACCOUNT_ID], how='left')

    df_score = df_score.repartition(PARALLEL_NUM)
    df_score = df_score.withColumn(FIELD_NAME_RW_RESULT,
                                   random_walk_with_restart(struct([df_score[x] for x in df_score.columns])))
    df_score = df_score.select(FIELD_NAME_ACCOUNT_ID, FIELD_NAME_RW_RESULT)
    df_score.write.option("overwriteSchema", "true").mode('overwrite').saveAsTable(TMP_TABLE_SCORE)

4.4 测试

我们使用如下规模的数据：

分区数（accountId）: 1
用户数: 30969
有向边的条数: 52091
图层数 2

spark集群配置：

spark.executor.memory 3g
spark.driver.memory 1g
spark.memory.fraction 0.3
spark.executor.cores 1

所有任务串行执行，即在仅有1个executor的情形下，执行时间为8分钟。

4.5 下一步的计划

经过测试，此算法适合计算小规模和中等规模的图（15万节点以下）。针对大型图，消耗的计算资源过于庞大，需要探索其他方式。因此，下一步的计划为：

探索图分割算法，对大型图进行切割。
探索大型图的特征提取算法，以减少数据量。Graph Embedding？