【推荐平台】基于Spark的大型社交网络重启随机游走算法实现

问题描述

目前，Zoom的业务涵盖了会议，电话，IM，邮件，日历，文档等等多个方面，事实上已经成为了一个多业务场景的办公平台。高效办公，是客户对于Zoom的期望。每天，数亿用户在Zoom各个业务线上产生了巨量的数据。如何利用好这些数据，真真正正地使办公变得高效，是亟需解决的问题。

Zoom Graph提供基于用户相关度的推荐和排序功能。例如，对于搜索场景，我们总是希望在搜索结果中，位于顶部的是用户最想要的数据，例如经常合作的客户，多次参加的会议等等。在联系人界面，我们希望为用户推荐经常一起工作的合作者，以及后续可能会建立合作的潜在客户。在AI助手中，我们需要搜集与用户提问尽可能相关的上下文。所有这些，都需要我们在用户的日常行为数据中，提取出与用户相关的实体对象，例如联系人，会议，日程等，并对其进行相关度计算，最终量化为分数。

解决思路

重启的随机游走算法

Karl Pearson在1905年第一次提出了Random Walk，如今已被应用在诸多领域：生态学，经济学，心理学，计算机科学，物理学，化学，生物学等。

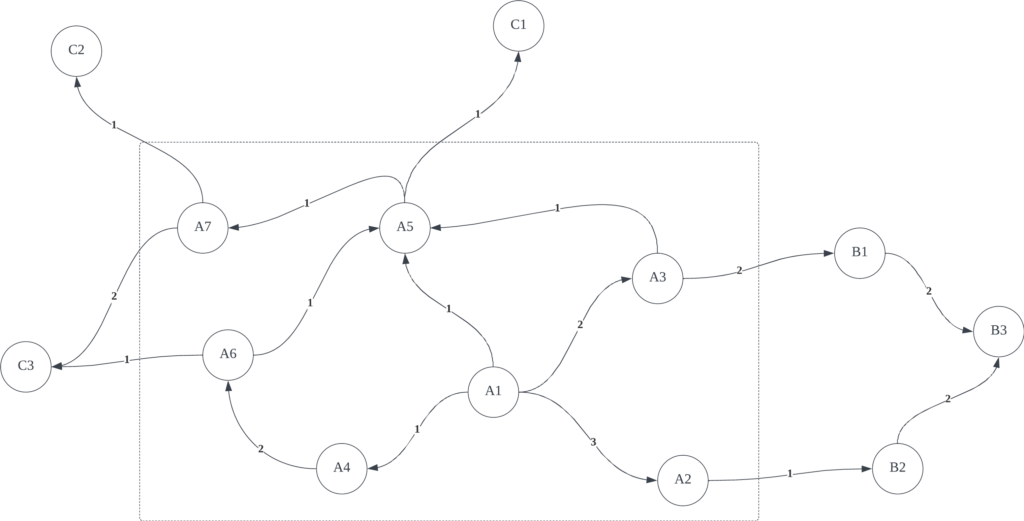
以用户为例，图中的每一个顶点代表一个用户，用户与用户间的有向加权边代表用户间的直接关联关系。我们需要获取与用户 A1 与其他用户之间的关联关系，并将其量化。

在该模型中，我们假设存在一个“探索者” S。S 从 A1 出发，在任意时刻 $t$ 都停留在图中的某一个顶点上。在下一时刻 $t+1$，S 必须从以下两个行动中选择一个执行：

行为1: 从当前顶点的所有邻居中，按照边的权重，以加权的概率随机选择一个顶点，并移动到该顶点。显然，权重越高的节点，S 有更高的概率访问。
行为2: 回到初始顶点 A1。显然，我们不希望 S 跑得太远。想象这样一个场景：在Zoom公司里，A1是开发，A5是产品，A7是销售，C2是我们的客户。我们一般不会认为C2是A1潜在的工作伙伴。

我们让 S 一直重复这样的选择（即每次选择一个行为，移动到下一个顶点；然后又选择一个行为，再跳转移动到下一个顶点），并记录 S 对每个顶点的访问次数。假设 S 前十次选择的节点序列是（A1, A3, A5, A1, A2, A1, A3, A1, A5, A6）。在前十次选择中，A1 被访问的概率为0.4，A2 被访问的概率为0.1，A3 被访问的概率为0.2 ，A4 被访问的概率为0.0，A5 被访问的概率为0.2，A6 被访问的概率为0.1 ，A7 被访问的概率为0.0。如果一直让 S 游走下去，可以想象，这样的概率会逐渐趋于稳定，那么最终将得到每个节点对 A1 的量化值。

数学语言

我们令图 $G=(V,E)$ 为加权有向图， $A$ 为邻接矩阵。假想 S 从初始用户 0 $v_0\in{V}$ 开始随机游走，考虑到时间是离散的，在第 $t$ 步， S 位于用户 t $v_t\in{V}$ ，在下一步，它从 $v_t$ 走到 $v_{t+1}$ 。因此，我们可以认为：$\forall{x,y\in{v}}, \ \forall{t\in\mathbb{N}}$

$$
\mathbb{P}(v_{t+1}=y \vert v_t=x)=
\begin{cases}
\frac{w_{xy}}{\sum_{i=1}^{v}w_{xi}}, & \forall{x,y\in{E}}, \\
0, & \text{otherwise}.
\end{cases}
$$

其中 $w_{xy}$ 是图 $G$ 中从用户 x 到用户 y 的边所对应的权重。定义 $p_t(v)$ 作为 S 在时间 $t$ 处在用户 v 的概率，我们可以描述概率分布 $P_t=(p_t(v))_{v\in{V}}$ ：

$$
P_{t+1}^T=MP_t^T
$$

其中 $M$ 表示转换矩阵，它是 $A$ 的列归一化后的分布。方程 $P^T=MP^T$ 的解（如果存在的话），表示 S 在时间趋于正无穷后，位于特定用户的概率。

我们引入重启的概念，在每次迭代时，S 还可以以固定概率 $r\in(0,1)$ 跳转到图中任意随机选择的节点来重新启动，这避免了行走陷入死胡同，并保证了平稳分布的存在。此外，我们可以将 S 的重新启动限制在特定用户 $v_0$，称为种子。这样做时，S 将探索以种子用户邻域为中心的图，并且最终的概率分布可以被视为种子用户与图中所有其他用户之间的接近度。形式上，单层图的随机游走方程可以定义为：

$$
P_{t+1}^T=(1-r)MP_t^T+rP_0^T
$$

向量 $P_0$ 是初始概率分布。因此，在 $P_0$ 中，只有单一种子用户的值为 1 。经过多次迭代后，向量之间的差异 $P_{t+1}$ 和 $P_t$ 变得可以忽略不计，最终达到平稳概率分布。

一些抽象

我们如何将Zoom中的用户关系，抽象为随机游走的图结构呢？很简单，我们根据用户日常操作的行为数据来为两个用户间建立边。例如，用户 A 和 B 一天内有过 5 次会议，我们为顶点 A 和 B 之间建立一条权重为 2 的边；用户 A 和 C 一天内有过聊天，我们为顶点 A 和 C 之间建立一条权重为 1 的边，以此类推。由于这样可能会导致两个用户间有多条边，因此我们再对两两用户间的所有边进行聚合，将权重相加。最终获得一张所有用户之间的有向加权图。

接着，我们遍历图上的所有顶点，分别将其设为种子顶点，使用重启的随机游走算法，计算种子顶点与其他顶点间的相似度，即为种子顶点与其他顶点的关联分数。

技术上的挑战

可伸缩性

现有的封装了重启的随机游走算法（Random Walk with Restart, RWR）的包，大多是本地计算的。它们都面临着可伸缩性的问题。当图的规模非常大时（当前我们的顶点数约为2亿），甚至无法在内存中完整存储转移矩阵，就更别提解矩阵方程，计算顶点相似度了。

对于分布式海量数据的计算，Spark是业内常见的解决方案。但是Spark并不原生支持RWR算法，其上的第三方库也没有支持（GraphFrame仅支持了PageRank算法，并不是我们需要的）。因此，需要我们自己去实现它。

幸运的是，我们可以使用数据源之间的Join操作，来传播“探索者” S 位置的概率函数：

首先，我们构建顶点和边来代表上图：

src	dst	weight
A1	A2	3
A1	A3	2
A1	A4	1
A1	A5	1
A2	B2	1
A3	B1	2
A3	A5	1
…	…	…

table_edges

id	totalWeight
A1	7
A2	1
A3	3
…	…

table_vertexes

我们构建表 st_position ，来代表 S 在 $t$ 时刻的位置概率。表结构如下：

name	description
seeds	seeds in RWR
currentVertex	The position of S at the current moment
probability	The probability that S’s position is under ‘currentVertex’ and seeded by ‘seeds’ at ‘t’ moment.

st_position

以A1作为种子为例，令 S 在任意时刻回到 A1 的概率为 a。在 $t_0$ 时刻，st_position内容初始化为：

seeds	currentVertex	probability
A1	A1	1

st_position_0

每次迭代，我们为表 st_position 应用以下操作：

SELECT seeds, currentVertex, sum(probability) as probability
FROM (
  SELECT  st_position.seeds AS seeds,
          table_edges.dst AS currentVertex,
          (1 - a) * st_position.probability * (table_edges.weight / table_vertexes.totalWeight) AS probability
  FROM    st_position
  INNER JOIN table_vertexes ON st_position.currentVertex = table_vertexes.id
  INNER JOIN table_edges ON st_position.currentVertex = table_edges.src
  UNOIN
  SELECT  id AS seeds,
          id AS currentVertex,
          a AS probability
  FROM    table_vertexes
)
GROUP BY seeds, currentVertex

在 $t_1$ 时刻，st_position 表的内容如下所示：

seeds	currentVertex	probability
A1	A1	a
A1	A2	(1 – a) * (3 / 7)
A1	A3	(1 – a) * (2 / 7)
A1	A4	(1 – a) * (1 / 7)
A1	A5	(1 – a) * (1 / 7)

st_position_1

在 $t_2$ 时刻，st_position 表的内容如下所示：

seeds	currentVertex	probability
A1	A1	a
A1	A2	a * (1 – a) * (3 / 7)
A1	A3	a * (1 – a) * (2 / 7)
A1	A4	a * (1 – a) * (1 / 7)
A1	A5	a * (1 – a) * (1 / 7) + (1 – a)^2 * (2 / 7) * (1 / 3)
A1	A6	(1 – a)^2 * (1 / 7) * (2 / 2)
A1	A7	(1 – a)^2 * (1 / 7) * (1 / 2)
…	…	…

st_position_2

我们以抽样的方式比较 $t$ 时刻和 $t+1$ 时刻 st_position 表的内容差异。若差异小于指定阈值，即可停止计算。

性能问题

上面的计算依据为公式：

$$
P_{t+1}^T=(1-r)MP_t^T+rP_0^T
$$

其中，$P^T$ 中的数据对应着表 st_position 中的内容，$M$ 中的数据对应着表 table_edges 中的内容。将上面的公式展开，可得：

$$
P_{t}^{T}=((1-r)M)^{t}P_{0}^{T}+r{\textstyle \sum_{i=0}^{t-1}}((1-r)M)^{i}P_{0}^{T}
$$

我们令 $\bar{P}_{t}$ 为在不重启的状态下，以 $P_{0}$ 为初始位置的情况下，$t$ 时刻 S 的概率分布。有：

$$
\bar{P}_{t}^{T}=M^{t}P_{0}^{T}
$$

则：

$$
P_{t}^{T}=(1-r)^{t}\bar{P}{t}^{T}+r{\textstyle \sum{i=0}^{t-1}}(1-r)^{i}\bar{P}_{i}^{T}
$$

假设图 G 为全联通图。当 $t$ 趋近于无穷大时，S 在图上分布较为分散，每个节点上的分布概率很低。因此，我们认为在这种情况下，$\bar{P}_{t}$ 近似为 0。上式近似为：

$$
P_{t}^{T}=r{\textstyle \sum{i=0}^{t}}(1-r)^{i}\bar{P}_{i}^{T}
$$

我们把目光拉回到上一节的SQL中：

SELECT seeds, currentVertex, sum(probability) as probability
FROM (
  SELECT  st_position.seeds AS seeds,
          table_edges.dst AS currentVertex,
          (1 - a) * st_position.probability * (table_edges.weight / table_vertexes.totalWeight) AS probability
  FROM    st_position
  INNER JOIN table_vertexes ON st_position.currentVertex = table_vertexes.id
  INNER JOIN table_edges ON st_position.currentVertex = table_edges.src
  UNOIN
  SELECT  id AS seeds,
          id AS currentVertex,
          a AS probability
  FROM    table_vertexes
)
GROUP BY seeds, currentVertex

下面的SQL等价于上面的求和通项 $(1-r)^{i}\bar{P}_{i}^{T}$

SELECT seeds, currentVertex, sum(probability) as probability
FROM (
  SELECT  st_position.seeds AS seeds,
          table_edges.dst AS currentVertex,
          (1 - a) * st_position.probability * (table_edges.weight / table_vertexes.totalWeight) AS probability
  FROM    st_position
  INNER JOIN table_vertexes ON st_position.currentVertex = table_vertexes.id
  INNER JOIN table_edges ON st_position.currentVertex = table_edges.src
)
GROUP BY seeds, currentVertex

此时，我们只需要将每次迭代的结果写入最终表中，再进行合并，即可。显然，相比于原始的SQL，由于每次迭代中少了一步Union的操作，使得表中的数据量大大降低，减少了很多重复计算。

此外，上文也提到，当 $t$ 趋近于无穷大时，S 在每个节点上的分布概率很低，该通项对于最终的结果贡献不大。这也提示我们，在每次Join操作中，可以针对表中 probability 值很低的记录进行过滤，因为其对最终结果贡献很低。因此，最终的SQL为：

SELECT seeds, currentVertex, sum(probability) as probability
FROM (
  SELECT  st_position.seeds AS seeds,
          table_edges.dst AS currentVertex,
          (1 - a) * st_position.probability * (table_edges.weight / table_vertexes.totalWeight) AS probability
  FROM    st_position
  INNER JOIN table_vertexes ON st_position.currentVertex = table_vertexes.id
  INNER JOIN table_edges ON st_position.currentVertex = table_edges.src
  WHERE st_position.probability >= 0.0001
)
GROUP BY seeds, currentVertex

数据倾斜

在测试阶段，我们发现了Spark运行缓慢，经常出现OOM的情况。在数据量上涨时，这种现象尤为明显。经过排查，发现存在异常数据。

在 table_edges 表中，某些顶点有数十万条边与其相连。在Join中，Spark会将相同Join Key的数据在同一个Executor中完成操作。这会导致某些Executor处理了太多数据，拉长整个任务的处理时间。当情况继续恶化，Executor可能无法将所有数据放入内存，进而导致OOM。

处理问题的方式也很简单。正常情况下，社交网络中每个用户维护的关系是有限的。20世纪90年代，牛津大学的人类学家罗宾.邓巴推断出：人类智力允许拥有稳定社交网络的人数是148人，四舍五入大约是150人，这就是著名的“邓巴数字”。因此，我们预先将每个顶点的边按照权重排序，只取前150条边即可。

下一步规划

探索多个实体间的随机游走算法。目前我们已经完成了用户间的网络构建，后续可以评估并接入会议，群聊等更多实体。
探索基于标签的相似性算法。我们可以使用用户基础属性和行为数据，为用户打上标签。例如职业，爱好，部门，等等。基于标签特征计算用户之间的相似度，作为目前的基于距离的方式的良好补充。
建立数据回流机制，评估算法准确度。

核心代码

# Databricks notebook source
# spark configurations
from pyspark.shell import spark
spark.sparkContext.setCheckpointDir("dbfs://checkpoint_dir/zrs/offline_score")

# table configurations
TABLE_ZRS_VERTEX = 'ml.zrs_user_vertex'
TABLE_ZRS_EDGE = 'ml.zrs_user_edge'
TABLE_ZRS_RWR_RESULT = 'ml.zrs_user_rwr_result'

# field names
FIELD_NAME_ACCOUNT_ID = 'accountId'
FIELD_NAME_LINK_WEIGHT = 'weight'
FIELD_NAME_OUT_WEIGHT_SUM = 'outWeightSum'
FIELD_NAME_VERTEX_ID = 'id'
FIELD_NAME_SCORE = 'score'
FIELD_NAME_RWR_SRC_VERTEX_ID = 'rwrSrcId'
FIELD_NAME_RWR_DST_VERTEX_ID = 'rwrDstId'
FIELD_NAME_RWR_SRC_VERTEX_ACCOUNT_ID = 'rwrSrcAccountId'
FIELD_NAME_RWR_DST_VERTEX_ACCOUNT_ID = 'rwrDstAccountId'
FIELD_NAME_VERTEX_SRC = 'src'
FIELD_NAME_VERTEX_DST = 'dst'
FIELD_NAME_RELEVANT_USER_RANK = 'rank'

# algorithmic parameter
PROB_RESTART = 0.3
LOW_PROB = 1e-4
MAX_ITE = 5
MAX_SRC_EDGE_PER_VERTEX = 150
MAX_DST_EDGE_PER_VERTEX = 750
CHECKPOINT_INTERVAL = 2

# COMMAND ----------

import pyspark.sql.functions as F
from pyspark.sql import DataFrame
from pyspark.sql import Window

def truncate_edge(df_edges: DataFrame, vertex_name: str, order_name: str, limit: int) -> DataFrame:
    window_spec = Window.partitionBy([vertex_name]).orderBy(F.desc(order_name))
    df_edges = df_edges.withColumn(FIELD_NAME_RELEVANT_USER_RANK, F.row_number().over(window_spec))
    df_edges = df_edges.filter(df_edges[FIELD_NAME_RELEVANT_USER_RANK] < limit)
    df_edges = df_edges.drop(FIELD_NAME_RELEVANT_USER_RANK)
    return df_edges

# COMMAND ----------

import pyspark.sql.functions as F
from pyspark.sql import DataFrame

def calculate_rwr_ite(ite: int, df_current_ite: DataFrame, df_v: DataFrame, df_e: DataFrame) -> DataFrame:
    df_current_ite = df_current_ite.filter(
        F.col(FIELD_NAME_RWR_SRC_VERTEX_ACCOUNT_ID) == F.col(FIELD_NAME_RWR_DST_VERTEX_ACCOUNT_ID))

    df_current_ite = df_current_ite.join(df_e,
                                         df_current_ite[FIELD_NAME_RWR_DST_VERTEX_ID] == df_e[FIELD_NAME_VERTEX_SRC],
                                         how='inner')
    df_current_ite = df_current_ite.join(df_v,
                                         df_current_ite[FIELD_NAME_RWR_DST_VERTEX_ID] == df_v[FIELD_NAME_VERTEX_ID],
                                         how='inner')
    df_current_ite = (df_current_ite.withColumn(FIELD_NAME_RWR_DST_VERTEX_ID, F.col(FIELD_NAME_VERTEX_DST))
                      .withColumn(FIELD_NAME_RWR_DST_VERTEX_ACCOUNT_ID, F.col(FIELD_NAME_ACCOUNT_ID))
                      .withColumn(FIELD_NAME_SCORE, F.col(FIELD_NAME_SCORE) * (1 - PROB_RESTART) * F.col(FIELD_NAME_LINK_WEIGHT) / F.col(FIELD_NAME_OUT_WEIGHT_SUM)))

    df_current_ite = (df_current_ite.groupBy([FIELD_NAME_RWR_SRC_VERTEX_ID, FIELD_NAME_RWR_DST_VERTEX_ID])
                      .agg(F.max(FIELD_NAME_RWR_SRC_VERTEX_ACCOUNT_ID).alias(FIELD_NAME_RWR_SRC_VERTEX_ACCOUNT_ID),
                           F.max(FIELD_NAME_RWR_DST_VERTEX_ACCOUNT_ID).alias(FIELD_NAME_RWR_DST_VERTEX_ACCOUNT_ID),
                           F.sum(FIELD_NAME_SCORE).alias(FIELD_NAME_SCORE)))

    df_current_ite = truncate_edge(df_current_ite, FIELD_NAME_RWR_SRC_VERTEX_ID, FIELD_NAME_SCORE, MAX_SRC_EDGE_PER_VERTEX)
    df_current_ite = truncate_edge(df_current_ite, FIELD_NAME_RWR_DST_VERTEX_ID, FIELD_NAME_SCORE, MAX_DST_EDGE_PER_VERTEX)

    df_current_ite = df_current_ite.filter(F.col(FIELD_NAME_SCORE) >= LOW_PROB)

    if ite % CHECKPOINT_INTERVAL == 0:
        df_current_ite = df_current_ite.checkpoint()

    return df_current_ite

# COMMAND ----------

import pyspark.sql.functions as F
from pyspark.sql import DataFrame

def combine_rwr_ite(ite: int, df_current_ite: DataFrame, df_all_ite: DataFrame) -> DataFrame:
    df_all_ite = df_all_ite.union(df_current_ite.select([FIELD_NAME_RWR_SRC_VERTEX_ID, FIELD_NAME_RWR_DST_VERTEX_ID, FIELD_NAME_SCORE]))
    df_all_ite = df_all_ite.groupBy([FIELD_NAME_RWR_SRC_VERTEX_ID, FIELD_NAME_RWR_DST_VERTEX_ID]).agg(F.sum(FIELD_NAME_SCORE).alias(FIELD_NAME_SCORE))

    if ite % CHECKPOINT_INTERVAL == 0:
        df_all_ite = df_all_ite.checkpoint()

    return df_all_ite

# COMMAND ----------

from pyspark.shell import spark
import pyspark.sql.functions as F

df_v = spark.sql(f'select {FIELD_NAME_VERTEX_ID}, {FIELD_NAME_ACCOUNT_ID}, {FIELD_NAME_OUT_WEIGHT_SUM} from {TABLE_ZRS_VERTEX}')

df_e = spark.sql(f'select {FIELD_NAME_VERTEX_SRC}, {FIELD_NAME_VERTEX_DST}, {FIELD_NAME_LINK_WEIGHT} from {TABLE_ZRS_EDGE}')
df_e = truncate_edge(df_e, FIELD_NAME_VERTEX_SRC, FIELD_NAME_LINK_WEIGHT, MAX_SRC_EDGE_PER_VERTEX)
df_e = truncate_edge(df_e, FIELD_NAME_VERTEX_DST, FIELD_NAME_LINK_WEIGHT, MAX_DST_EDGE_PER_VERTEX)
df_e = df_e.checkpoint()

df_rwr_ite = (df_v.withColumn(FIELD_NAME_RWR_SRC_VERTEX_ID, F.col(FIELD_NAME_VERTEX_ID))
              .withColumn(FIELD_NAME_RWR_DST_VERTEX_ID, F.col(FIELD_NAME_VERTEX_ID))
              .withColumn(FIELD_NAME_RWR_SRC_VERTEX_ACCOUNT_ID, F.col(FIELD_NAME_ACCOUNT_ID))
              .withColumn(FIELD_NAME_RWR_DST_VERTEX_ACCOUNT_ID, F.col(FIELD_NAME_ACCOUNT_ID))
              .withColumn(FIELD_NAME_SCORE, F.lit(PROB_RESTART)))

df_rwr_ite = df_rwr_ite.select([FIELD_NAME_RWR_SRC_VERTEX_ID, FIELD_NAME_RWR_DST_VERTEX_ID, FIELD_NAME_RWR_SRC_VERTEX_ACCOUNT_ID, FIELD_NAME_RWR_DST_VERTEX_ACCOUNT_ID, FIELD_NAME_SCORE])
df_rwr_all = df_rwr_ite.select([FIELD_NAME_RWR_SRC_VERTEX_ID, FIELD_NAME_RWR_DST_VERTEX_ID, FIELD_NAME_SCORE])

for ite in range(0, MAX_ITE):
    df_rwr_ite = calculate_rwr_ite(ite, df_rwr_ite, df_v, df_e)
    df_rwr_all = combine_rwr_ite(ite, df_rwr_ite, df_rwr_all)

df_rwr_all = (df_rwr_all.withColumn(FIELD_NAME_VERTEX_SRC, F.col(FIELD_NAME_RWR_SRC_VERTEX_ID))
              .withColumn(FIELD_NAME_VERTEX_DST, F.col(FIELD_NAME_RWR_DST_VERTEX_ID)))
df_rwr_all = df_rwr_all.select([FIELD_NAME_VERTEX_SRC, FIELD_NAME_VERTEX_DST, FIELD_NAME_SCORE])
df_rwr_all = df_rwr_all.filter(F.col(FIELD_NAME_VERTEX_SRC) != F.col(FIELD_NAME_VERTEX_DST))

df_rwr_all.write.option('overwriteSchema', 'true').mode('overwrite').saveAsTable(TABLE_ZRS_RWR_RESULT)